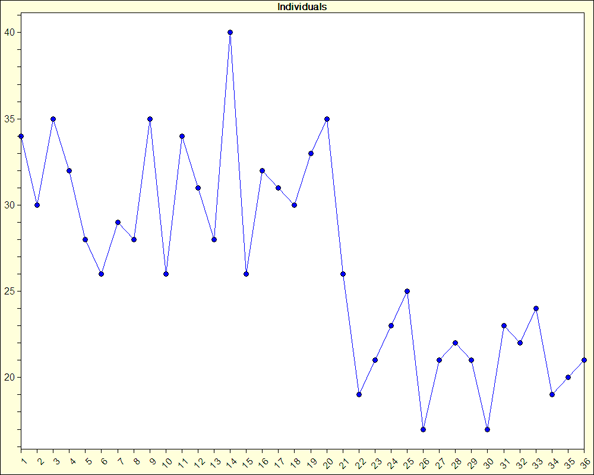
Cpk has been a popular capability index for many years and perhaps because of its momentum it continues to remain popular. But is it the best index to use? Answering this question assumes that there is one best index, which is a different discussion altogether. Let’s agree that there several other useful capability indices. Two other indices that can be beneficial are Ppk and Cpm. As mentioned in a previous article on Cpk, “Cpk or Ppk: Which should you use,” Cpk uses only the estimated sigma to measure variation. While this is acceptable, the estimated sigma can be artificially low depending on the subgroup size, sample interval, or sampling plan. This in turn can lead to an over-inflated Cpk. For a process that drifts, such as the process shown in the chart below, the estimated sigma will usually be artifcially low. This is because the estimated sigma looks at only variation within subgroups.

Ppk, on the other hand, uses the standard deviation from all of the data. We can call this the sigma of the individual values or sigmai. Sigma of the individual values looks at variation within and between subgroups. For a process that exhibits drifting, estimated sigma would not pick up the total variation in the process and thus the Cpk becomes a cloudy statistic. In other words, one can not be sure it is a valid statistic. In contrast to Cpk, Ppk, which uses the sigma of the individual values, would pick up all the variation in the process. Again, sigmai uses between and within subgroup variation. So if there is drifting in the process, sigmai would typically be larger than the estimated sigma, sigmae, and thus Ppk would, as it should, be lower than Cpk.Here is a quick review of the formulae for Cpk and Ppk:

We should be concerned with how well the process is behaving, therefore Ppk might be preferred over Cpk. Ppk is a more conservative approach to answering the question, “How good is my process?” Watch for a future article discussing the relatively new capability index, Cpm, and how it stacks up against Cpk and Ppk.